プロシージャルという言葉は、もともと「手続き型」という意味で、プログラムのアルゴリズムによって特定の作業や処理を行うプロセスを指す言葉です。例えばゲーム等では、主人公が冒険に旅立ち、その風景は状況に応じて次々と展開されていくわけです。この画面を一つ一つプログラムで描いていくには、膨大な量になります。だからアルゴリズムを使って、自動的に地形や場面を生成する方法が開発されました。これまで書いてきたblogの例では、「プレグナンツとベイズ推定、その応用について」の中で示した文様の動画、「「再帰」とは、L-system, ・・・」の中のフラクタルの動画、はプロシージャルと言えます。一つのプログラムからいくらでも文様が作れていきます。こうした狭義の意味から拡張され、AとBという別々のモノに関連をつけて、Aを変えるとBも変わるといった場合にもプロシージャルというようになってきました。こちらの場合ですと、非常に広い範囲がプロシージャルということになります。このblogでは、この広い意味でプロシージャルという言葉を使います。ただしプロシージャルと言う言葉には、「関係性」というニュアンスが伴っています。これについて以下説明致します。
仏教の「諸法無我」の説明に「車輪」の例がでてきます。これとプロシージャルは非常によく似ています。この例をかいつまんで説明すると次のようになります。車輪の働きは「回転して荷物を運ぶ」機能ですが、それは外枠の車、スポーク、軸受け等の様々な構成要素が関連しあってできた集合体です。一部が壊れて、ばらばらになれば、それは車輪ではなくなり、荷物を運ぶという機能も失われます。「私」というのもこれと同じです。様々な部分とそれらの関係性(心臓や手足のような肉体的な関係だけでなく、人との関わり等も含みます)によって、私が作られており、それらの状況によって私は常に変化しており、これが「私」です、というような固定された存在ではない(諸法無我)、と言うような説明がなされます。まさにTouchdesignerやMAXでは、個々の構成要素が用意されており、これを組み合わせることで、別の機能を発揮させるものです。また、電子回路も同じです。抵抗やコンデンサ、インダクタ、トランジスタ、ダイオードといった要素を組み合わせることで、別の機能を作ります。マイコンやコンピュータもこれらの要素で作られているのです。このようなところまで拡張すると、なんでもありのように思えますが、「関係性」に着目した概念であるということが重要です。要素を集めたらできる、という意味ではありません。実際、電子回路もプログラムも、この関係性をどう作るのかに工夫のしどころがあります。
そして、もう一つ「諸法無我」の説明には重要な観点が入っています。それは、常に関係性が変化しているから、これが「私」ですという決まった「私」と言うものはない、というところです。プロシージャルで言うなら、構成要素は同じ、あるいはプロセスの手順は同じなのだけれども、関係性が変わることで、様々な形や模様になったり、動きに成ったりするところに関連します。そしてここに「未知」が生じます。フラクタルやカオス、今後説明していく「擾乱を伴う反復系」といった非線形現象はもちろん「未知」が発生します。しかしそうした非線形性がないものでも、状況によって新しい課題が生じ、そのために新たな機能をつくるために新たな構成が必要になる、といったことが生じます。これもまた「未知」です。ですから、「関係性」を加えていくとたいていが「未知」に出会います。そして、こうしようか、ああしようかというように、モノとのフィードバックが生じるようになります。このように作り手は、モノとのコミュニケーションしているわけですが、作製したモノが、別の人にとってモノとのコミュニケーションが働くかはまったくの別問題です。多くは失敗に終わりますが、こうした考えはヒントになると思います。
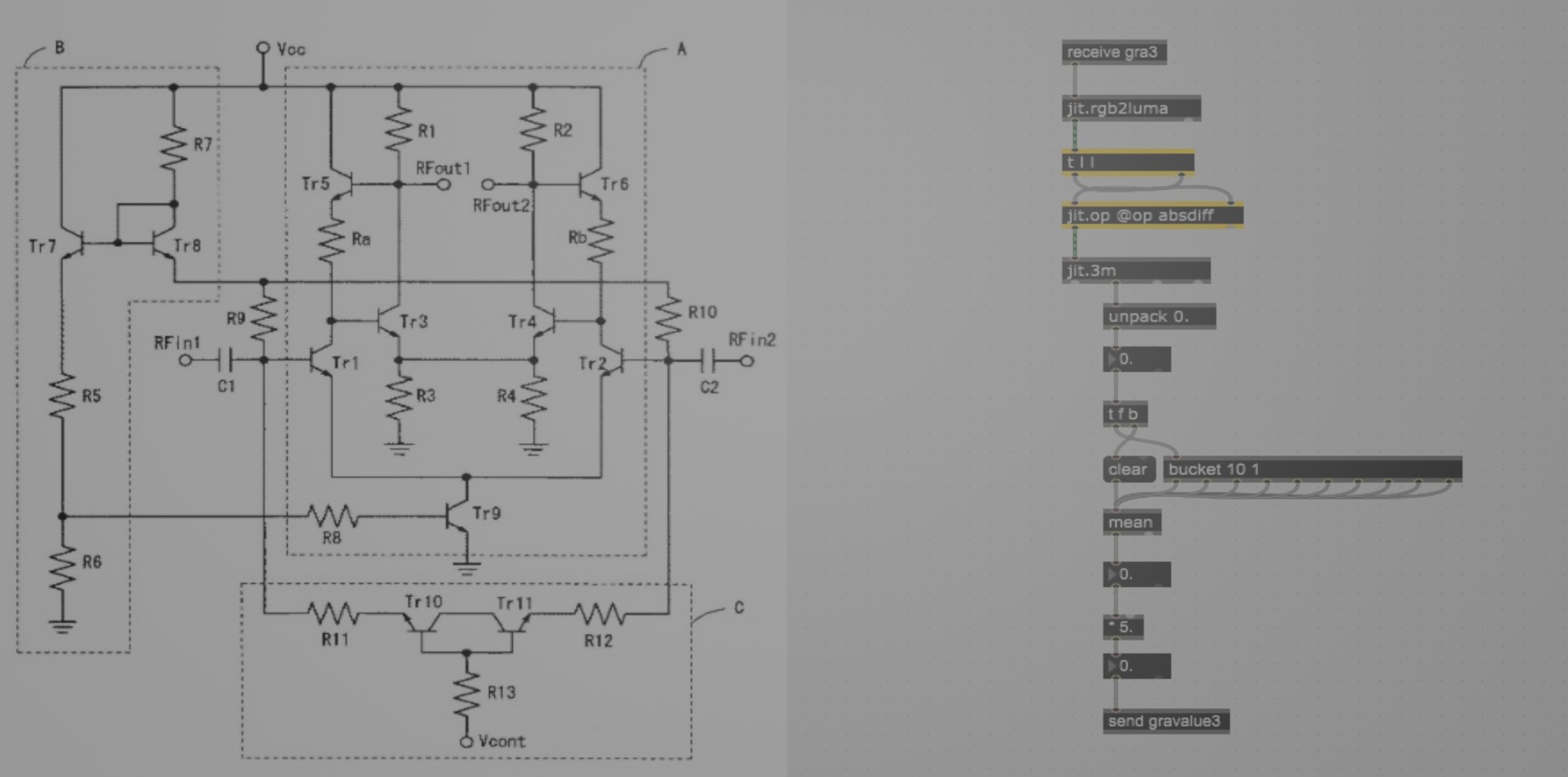
今回のblogの図は電子回路とMAXのプログラムの例です。要素に関係性を与えることで機能を作る例として挙げました。電子回路は特開2011-119968 利得可変回路の代表図面です。差動系の直結合回路で負荷に電流源を活用したフィードバック回路を備えています。回路の説明はともかく、抵抗とコンデンサとトランジスタの組み合わせでできています。これにインダクタやダイオードを加えて、これだけでほとんどの回路が作られます。そして電子回路は今や、あらゆる電子機器に入って機能しています。たったこれだけの要素の組み合わせで、インターネットも動き、飛行機も飛んでいるのです。この組み合わせで無限の機能が作れるのです。プロシージャル(関係性)には驚きます。かつて学校で、「基礎的な要素が大切で、後はこれらを組み合わせればできます」と言ったような教育を受けたように思いますが、まったくのでたらめです。関係性に大切さがあるのです。もう一つの画像はMAXのプログラムの例です。映像の、前のフレームと今のフレームとの差を数値として出力するプログラムです。画像の一部を受け取って白黒に変え、前のフレームと今のフレームとの差の絶対値を得ます。次にその絶対値に対して全てのセルの平均値を求め、さらにその値の移動平均を求めています。個々のブロックには役割があり、それぞれがオブジェクト指向プログラムのクラスにあたります。これらのクラスに関連性を与え(つないでいくことに相当します)、前のフレームと今のフレームとの差を求める機能を作っています。


コメント