はじめに
データの値からノート・ナンバー(ピッチ)をどうして得るかの問題を説明致します。そのために必要な音楽理論、そしてその部分のプロブラムを解説致します。とても基礎的ですがデータから音楽を作るには必須です。
音楽理論の基礎:スケール
この節ではスケール(音階)の説明を致します。次の図に鍵盤とノート・ナンバーの関係を示しています。
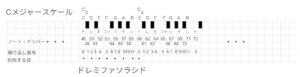
鍵盤の一番左のノート・ナンバーは0で一番右が127です。これは黒鍵も含めての数です。そしてノート・ナンバー0はC-1と呼ばれています。1オクターブ高いドがC0、更に一オクターブ高いのがC1と続いていきます。何故かしりませんが、C-1からはじまることに注意が必要です。
データから曲を作るのは、結局入力データを鍵盤のどこに当てはめるかという問題です。ここで重要なのがスケール(音階)です。ノート・ナンバーの決め方の前にスケールについて説明致します。先回のblogでも少し触れています。ピアノ、ギター、ベース等、様々な楽器があった場合、どれも同じスケールで演奏すると、曲っぽく感じます。同じスケールの音でないモノが入ると違和感を感じます。何故人はそう感じるのか、和音と関係していると思いますが、明確には分っていないと思います。これは人の特性です。
鍵盤はドからシまでの音が繰り返されており、ドからシまでの中に音は黒鍵を含めて数えると0~11の12音です。この0~11を1オクターブといいます。そして例えばC3のドと次のC4のドとの関係はC3のドの2倍の周波数の音がC4です。この関係は勿論ドだけではありません。図の下側に繰り返し番号と書いた番号を書いています。0~11を繰り返しています。同じ番号の音は左から右に対して2倍ずつ周波数が高くなっています。音楽には度数という数え方があります。これはある音からある音まで、どれだけ番号が離れているかということです。例えばドとレなら0と2なので2度離れています。レとファなら2と5なので3度離れていることになります。ミとファとの関係は4と5ですから、1度離れています。この関係はメジャー(長調)かマイナー(短調)かを決める重要な意味を持ちます。ドレミファソラシドのとなりの音との関係が何度離れているかを見て行きましょう。隣の音が2度離れている場合を全音、1度離れている場合を半音といいます。ドレミファソラシドの関係をみていくと、ドとレは2音、レとミは2音、ミとファは1音・・・としていくと、ドレミファソラシは「全・全・半・全・全・全・半」となっています。これを繰り返し番号で書くと(0, 2, 3, 5, 7, 8, 10, 0)となります。この組み合わせになるスケールをメジャー(長調)と言います。ドレミファソラシドはそれぞれCDEFGABCと対応しています。ドはCでもあります。ドレミファソラシドはドからはじまった数え方なので、Cメジャースケールと呼ばれます。次にラからはじまるスケールを見てみましょう。次の図を見てください。

つまりラシドレミファソラです。CDEFGABを当てはめると、ラはAに当てはまりますので、ABCDEFGAとなります。そして繰り返し番号をみていただくと、Aから始まるのでAを0として書いています。それではラシドレミファソラの隣の音が何度離れているか見てみましょう。ラとシは2度、シとドは1度、ドとレは2度・・・となっていきます。これを全音と半音で書くと、「全・半・全・全・半・全・全」となります。繰り返し番号で書くと(0, 2, 3, 5, 7, 8, 10, 0)になります。この組み合わせをマイナー(短調)と言います。従ってラシドレミファソラを使うスケールをAマイナースケールと呼びます。音階の始まりをどこにするのか、そして、隣の音との関係が、「全・全・半・全・全・全・半」(0, 2, 4, 5, 7, 9, 11, 0)か、「全・半・全・全・半・全・全」(0, 2, 3, 5, 7, 8, 10, 0)かでスケールが決まります。音階のどこから初めても、このメジャーとマイナーの組み合わせに必ずなります。特にCメジャースケールとAマイナースケールとは、構成している音は最初をどこにするかが違うだけで同じ音を使っています。この関係を平行調と言います。
それでは、Aメジャースケールというのはできるのでしょうか。勿論できます。A即ちラを初めとして、「全・全・半・全・全・全・半」(0 2 4 5 7 9 11 0)となる関係がそいうです。図の繰り返し番号を追っていってください。そうすると、「ラ・シ・ド♯・レ・ミ・ファ♯・ソ♯・ラ」が対応していることが分かると思います。つまりこの音階がAメジャースケールです。
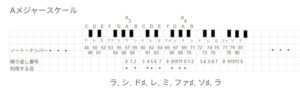
ここで、繰り返し番号からわかるように1オクターブの間にある音は12音です。しかしスケールと言っている音は7音となっています。12音全部の音を使って曲を作るわけではなくて、7音の決まったスケールで曲を作るのが基本です。勿論この7音の一つ上のオクターブや、一つ下のオクターブのように、何オクターブかを使って曲は作られます。何故12音でなく7音なのが、何故そのほうがシックリくるのか、それは分っていないと思います。これまで、スケールの音の中で演奏すると言ってきましたが、別のスケールの音を入れることは実際の音楽ではしばしばあります。別のスケールの音は聴くと違和感がありますが、これが感情の変化や、注目すべきべ場面等に対応して使うと、感情を動かしたり、注目を集めたりすることになります。別のスケールの音を入れることは、上級のテックニックです。このblogでは扱いません。
また、しばしばメジャースケールは明るい感じで、マイナースケールは暗い感じと言われます。実際そう感じることはしばしばあります。これは和音を扱う時はより分かりやすくなります。ベルグソンが述べているように音楽は持続があります。前の音と今の音の関係が印象にとって大切です。このため、和音の流れが大切になります。これがコード進行です。コード間の関係も気持ちを動かすことと関連して語られていますが、これも何故そうなのかは、わがっていないと思います。音楽の多くは、こうすればこんな感じになるということが長い歴史の中で多くの知見として蓄積されています。しかし人は何故そう感じるのかは、わかっていないことが多いようです。
7音を使うのが通常ですが、日本の伝統音楽には5音を使う音楽が多く知られています。5音を使う音楽は確かになんとなく日本的な感じがします。これを5音ですからペンタトニックスケールといいます。代表的なのが、黒鍵だけを使う演奏法です。最後にこれについて検討しておきます。まずBメジャースケールを考えてみましょう。次の図をみてください。
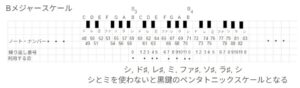
Bからはじまるのでシが繰り返し番号の先頭です。そしてメジャーですから、「全・全・半・全・全・全・半」(0 2 4 5 7 9 11 0)の関係です。すると「シ, ド♯, レ♯, ミ, ファ♯, ソ♯, ラ♯、シ」となります。ここで、シとミを使わない規則にすると、「ド♯, レ♯, ファ♯, ソ♯, ラ♯」となって黒鍵だけのBメジャースケールになります。Bメジャーケールの図を見て、D♭の音が黒鍵ですので、こっから初めても黒鍵だけになるかもしれないと思われた方もいらっしゃるでしょう。その通りです。D♭メジャースケールを検討してみましょう。

レの♭、これはド♯と同じですが、これを繰り返し番号0にして、メジャースケールですから、「全・全・半・全・全・全・半」(0 2 4 5 7 9 11 0)の構成音にすると。繰り返し番号に対応する音は「レ♭(ド♯), レ♯, ファ, ファ♯, ソ♯, ラ♯, ド, レ♭(ド♯)」になります。これがD♭メジャースケールです。ここで、ファとドを使わないとすると、「ド♯, レ♯, ファ♯, ソ♯, ラ♯, ド♯」黒鍵だけとなり、Bメジャースケールの黒鍵だけを使う場合と全く同じになります。
ノート・ナンバーも求め方
それでは入力データがスケールにあったノート・ナンバーに変換される部分のプログラムを検討してみましょう。この節の内容は「MAXの教科書 ノイマンピアノ(赤松正行+佐近田展康)株式会社リットーミュージック」を参考にしています。「ずらし値」という考えを取り入れたこと、tableの説明を詳しく行い、Cメジャースケール以外でも扱えるようにした点がオリジナルです。
前節のCメジャースケールの絵を見てください。繰り返し番号0~11の12音が繰り返しています。ですので入力値xに対して12で割って商と余りでx、即ちノート・ナンバーを指定することができることがわかります。商は何回目の繰り返しであるのか、余りはその繰り返しの中の何番目かを表すことになります。例えばセンサー値が50であるとすると、12で割って商が4余り2となるので、4回目のオクターブで余り2となります。それでは次にAマイナースケールの鍵盤の絵を見てください。Aマイナースケールは繰り返し番号はラ(A)からはじまるります。ラ(A)が基準です。そのためA-1を0として数えると、A0が12, A1が24, A2が36, A3が48となります。C-1を0とした数えたのがノート・ナンバーです。これはCから数えたA3は57となっているので、48 = 57 -9で9マイナスにする必要があります。この9は何かというとCから数えてAは何番目かという繰り返し番号です。つまり、基準をAを0として数えるためには、最初Cから数えたAの繰り返し番号を引いておく必要があります。これを「ずらし値」と呼ぶことにします。Aの「ずらし値」は9ということです。それではノート・ナンバー50はどうかけるでしょうか、A(ラ)を基準とするとと50-9で41番目になります。41を12で割ると商が3であまりが5です。Aを基準として3回目のオクタ―ブあまり5となります。それでは元のノート・ナンバー50の値にするにはどうればいいでしょうか。それは12*3+5の計算をした後に「ずらし値」である9を加えれば50になります。Aを例に検討しましたが、どのスケールでも同様に考えることができます。
先ほど音は0~11の12音なのに、スケールは7音であることを述べました。これは0~12が入ってきた際に、どこかの音を2回あるいは3回数えることにして7音に変換します。これが変換テーブルで。下図のtableを見てください。
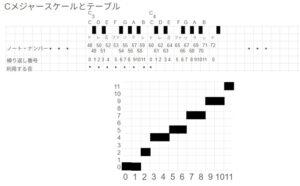
横軸は0~11の繰り返し番号、縦の0~11は横をどの値に割り付けるかを示します。繰り返し値0番のドの音はドの音に割り付けますから(0,0)です。繰り返し1はド♯ですが、ドレミファソラシドの7音に割り付けるのですから、ドでもレに割けてもいいですが、ドに割り付けましょう。ドの繰り返し番号は0です。ですので(1,0)になりなす。横軸繰り返し番号2のレはレに割り付けるので繰り返し番号は2です(2,2)、横軸3はレ♯です。これはミに割り付けましょうミは繰り返し番号4ですから(3, 4)となります。横軸4番はミですか4番のミに割り付けます(4,4)、横軸5ファは同じくファに割り付けれますので'(5,5)、横軸6のファ#は7番ソでもいいですが、5番ファに割り付けましょう(6,5)、横軸7番ソは7番ソに割り付けますので(7,7)、8番ソ♯は7番ソに割り付けると(8,7)、横軸9番ラは9番ラに割り付け(9,9)、10番ラ♯は9番ラに割り付けましょう(10, 9), 11番シは11番シでいいので(11,11)となります。これでCメジャーースケールで12音を7音に割り付ける変換テーブルができました。この説明でわかるように7音に割り付け方は複数通り考えることができます。
次に「ずらし値」が必要な場合を検討してみましょう。黒鍵だけをつかうペンタトニックのD♭メジャースケールを同様に割り付けてみます。

黒鍵だけですから12音を5音(ド♯, レ♯, ファ♯, ソ♯, ラ♯)に割り付けることになります。D♭即ちC♯はCから1つ上の音ですので、「ずらし値」は1です。つまりド♯(C♯)を基準にするには、最初-1を引くことになります。それではテープを作製してみましょう。繰り返し番号横軸0のド♯はそのままド♯に割り付ければいいので(0,0), 横軸1のレもド♯に割り付けましょう(1,0)、横軸2のレ♯はそのままレ♯に割り付ければいいので(2,2)になります。横軸3ミは、レ♯に割り当てましょう(3, 2)、横軸4のファですが、これはレ♯でもファ♯にも割り付けることができます。ここではレ♯にしておきます(4,2),、横軸5のファ♯はそのままファ♯に割り付けます(5,5)、横軸6のソもファ♯でもソ♯でも割り付けれます。今回はファ♯に割り付けます(6, 5)、横軸7はソ♯ですので、そのままソ♯に割り付けます(7,7)、横軸8のラはソ♯に割り付けておきましょう(8, 7)、横軸9はラ♯は同じくラ♯へ割り付けます(9.9)、横軸10, 11のシとドもラ♯へ割り付けます(10, 9), (11, 9)です。これでD♭メジャースケールのファとドを抜いたペンタトニックのスケール表ができました。基準はD♭で「ずらし値」1で初めに引き算したので、これをCを基準としてノート・ナンバーに戻すために、「ずらし値」1を加えます。どんなスケールもこの方法で割り付けることができます。
さてこれをプログラムにしたのが次の図ですMAXによります。
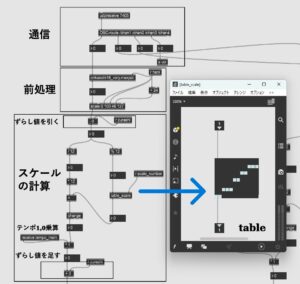
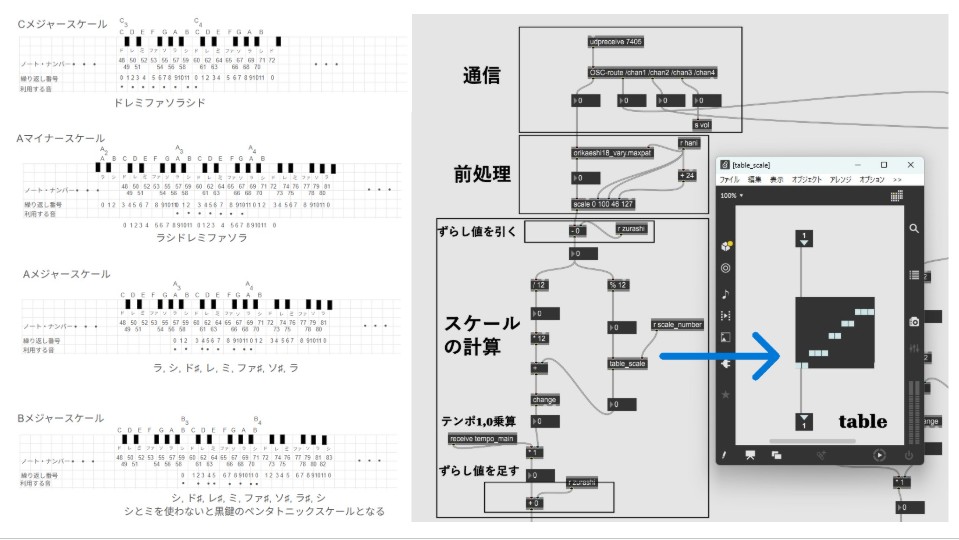
通信部分は前回述べました。TouchDesignerから信号が入ってきます。前処理はマッピングのための処理で後で説明致します。「ずらし値」は上述してきたド(C)からのずれ値です。スケール計算部分を説明致します。左側の経路は12で割って12で掛けていますが、これは割算の時整数にするためです。12で割った値を整数値にして何回目のオクターブかを求め、それを12で掛けています。12で割った余りをスケールに割り付けるのが、上述してきたtableです。そして12を掛けた値とtableからの値を足して、割り付けた値を求めています。その後Cからの数になるように「ずらし値」を足してノート・ナンバーができます。テンポの101010・・・を掛けて1の時にノート・ナンバーが出力されます。長い説明になってしまいましたが、ようやくノート・ナンバーを作ることができました。
前処理
前処理と書いた部分について解説致します。MIDIで音楽を作る場合、ノート・ナンバーは0~127に制限されています。そして実際音楽を作る場合、極端に低い音や高い音はめったに使いません。通常2~3オクターブの中で曲を作ることが多いと思います。入力のデータをその範囲に収めるのが前処理です。今回の場合、最初の前処理はTouchDesignerで行い。それを受けてMAXで行います。入力信号の範囲をノート・ナンバー48~84に割り振るとといったようなスケールを使うマッピングが一般的ですが、折り返しというオリジナルな前処理をしています。例えばデータ信号が200という値であった場合を考えてみます。例として0~48の3オクターブ分で曲を作ることにします。200は48より大ききので200-48で152、まだ大きいの152-48で104、さらに104-48で56、まだ大きいので56-48で8になります。8は48以下になったのでこの値を使います。こうすることで、どんな大きな入力があっても0~48の値に収まります。そしてその後、scaleオペレータで、0~48を48~84(3オクターブ分)あるいは48~72(2オクターブ)の聞き取りやすい範囲にマッピングします。今回の場合は、MAXにデータを渡す前にTouchDesignerでも前処理をしています。温度は-5°~40°ぐらいですか、これを-10°~200°ぐらいにマッピングして、それをMAXに渡すと折り返しの効果が表れます。この折り返しは、音楽に抑揚を与える効果がしばしば生じます。これで単調な印象を防ぐのに役立ちます。TouchDesigner及びMAXでの前処理によって、曲の印象は随分変わります。ノート・ナンバーを決める部分は決まった計算方法なので変えることができませんが、前処理は様々な工夫ができます。
MIDI信号の作製
ノート・ナンバーをベロシティやデュレーション等と合わせてMIDI信号にして、それをMIDI音源に送ります。この部分は上記MAXの教科書の内容をそのまま使うことができます。notooutオペレータのMIDI送信ポートの設定には、初期状態ではMicrossoft GS wavetable synthになっています。私の場合は先回のblogで話したように、MIDI音源にSonic Cellを使うので。パソコンとSonic CellをつなぐインターフェースであるUM-ONEを選択します。
データは2月, 7月, 10月の時間毎の気温データでした。それぞれに対して同じプログラムを並列に作っています。Sonic Cellでは2月がピアノJD-800 7月がアコスティックギター SC Brt Nylon, 10月がバス Sonic Ac Bsに設定しました。それではD♭メジャーのペンタトニックスケールを用いた場合、Cメジャースケールを用いた場合、Aマイナースケールを用いた場合、の温度データによる音楽を聴いてください。
D♭メジャーのペンタトニックスケールの場合
Cメジャースケールの場合
Aマイナースケールの場合
コード進行
上述ではデータをスケールに従って加工し、それを楽器に当てはめて演奏することを紹介してきました。よく聞く音楽はスケールでなくコード進行を使います。つまり和音です。和音について話すと長くなので省略して、スケールの関係を簡単に述べます。和音は3つあるいは4つの音を同時に鳴らすことで、その関係はドミソのように決まっています。ですので、7音や5音に割り当てていたスケールを和音の音しか鳴らないように割り付ければ、和音のなかから音を選択できるようになります。つまりtableと「ずらし値」を変えればいいのです。別のデータからは別の楽器をならしますが、それもドミソから選択させます(同じ和音から選択させる)。そうすると、複数の楽器で和音を形成することになります。考え方は上述した節と同じです。そして例えば1小節ごとに和音を変えていくとコード進行が扱えるようになります。
まとめ
データを音楽に変換するには、今回紹介してこなかった、リズムをどう作るか、抑揚をどのようにつけるか、アクセントをどこにいれるか、と言った内容も重要です。しかし最も重要なのは、様々なデータを0~11の繰り返しの中に如何にマッピングするかという問題に帰着すると思います。今回紹介したのはその考え方です。パソコンでは映像でモノの動きが作れます。そしてその作製したモノ対して何かを作用させ、その時の変化が観測できます。それを音楽に変換すると、モノの変化の様子を音楽で表現したことになります。それをモノがアクションに対して答えてくれたと解釈すると、モノとのコミュニケーションにつながると思っています。音楽や音を使ったモノとのコミュニケーション、これはMonogokoroが追求するテーマの一つです。

コメント