2つ前のブログで、「再帰」についてL-systemやフラクタルを解説し、繰り返しにより作製する形状について述べました。再帰は繰り返しを活用して作る非線形性ですが、今回話す非線形性は再帰を使いません。今回メインに話すのはディスプレイスメントという技術です。この技術は自然界にはありません。そしてここで現れる非線形現象はコンピュータ内に現れる現象です。L-systemは自然現象を模倣しようとして生み出されたシミュレーションです。模倣した非線形性です。フラクタルは自然界にある非線形性で、それを真似た現象です。ディスプレイスメントで生じる非線形性は、人が作ろうとした非線形性でも、自然界にある非線形性でもありません。コンピュータを使うことでかってにできてしまう非線形性で、コンピュータ固有の世界を垣間見せる興味深い現象です。
まず、非線形というのがどんな現象なのかを極簡単に述べておきます。最初に習う非線形性はx2でしょう。ここにa=sinω1t, b=cosω2tをいれると、sin2ω1t+ cos2ω2t+2sinω1t ・cosω2tとなり、一項目から2ω1, 2項目からは2ω2の2倍波が現れ、掛け算の項からは、ω1―ω2 及びω1+ω2のミキシングの項が現ます。入力した周波数でなくその2倍の周波数がでてくるということは、2倍の周波数が作られたということです。そしてミキシング項は、基本波であるω1, ω2でなく、新しい周波数ω1―ω2 及びω1+ω2であり、これも入力した周波数でない周波数が作られたのです。これを使って変復調の原理が説明されます。非線形性によって新たな周波数が作られるという解釈は、現象を使ってインターラクションを作製する人にとって非常に大切な視点です。与えた元を利用して何かを作る時に、この非線形性を活用すると、何かが生み出されるということなのです。x2の例で、こんどはa+bを代入してみましょう。a2+b2+2abです。これを数字が変わっただけとみてはいけません。a2とb2は指数関数ですし、abは積です。指数関数でないものを入力したのに、和を入れたのに、指数と積が生み出されたのです。性質が違ったものが作られたのです。このように、新たな関係を生成する。これが非線形性の本質です。入力自体が非線形であり、それを演算する内部にも非線形性があると、何が出力にでてくるのか予測がつかなくなります。これが意外性を作ることになります。
それでは平面や立体の場合はどうでしょうか、簡単に言えば自分の高さが、自分だけで決まらず、自分の隣接する場所の影響、あるいは、遠くにある場所の影響を受けて、生成消滅したり、高くなったり低くなったりし、予測がつかない動きになります。周りの影響を受ける現象が生じます。自分の周囲の影響を受けて次の動きが決まる、生成したり消滅したりする、life-gameのConwayがそうでしたね。Conwayは非線形ということです。そして自分自身がコピーされて入れ子構造を作るのがフラクタルでした。自分自身が大きくなったり小さくなったりするだけで決まらないところが非線形なわけです。L-systemは、自分自身の一部が繰り返される入れ子構造でしたね、これによってフラクタル同様、自分自身が大きくなったり小さくなったりするだけで決まらない複雑な形になっていきます。つまり新しい形を生成していっているのです。単に周りの影響を受けるだけでは非線形性とはいえません。となりの動きが1動いたとき、自分には0.2倍した影響が足される。といった場合は線形です。周囲の影響を受けるのだけれども、その受け方は、指数や対数、掛け算のような、足し算、引き算ではない関係が入っていることが必要です。これによって、非線形が在る場合は、平面でも立体でも予測のつかない凸凹ができます。それを見ると、「へーこんな形になるんだ」という意外性を感じます。このように非線形を使うと、与えたものだけでなく、新しい関係をつくりだします。これによって意外性ができるということです。調和や安定を与えるのに線形性を利用します。線形性の例の代表は市松模様でしょう。意外性はありません。しかし安定でどこまでも同じ構造が続いていきます。永遠と調和の象徴です。
ディスプレイスメントの説明をしていく前に、これで作る非線形性がとんなものが、最初に見ていただきまましょう。以下の3枚の画像を示します。



この形状を作るのに必要なプログラムは、
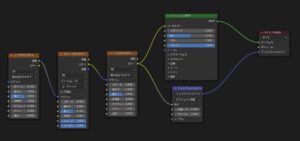
これだけです。このパラメータを変えると、いくらでも作れます。私はこのプログラムを自力で見つけました。大変驚きました。ポイントはディスプレイスメントとボロノイテクスチャーとノイズテクスチャーの組み合わせです。AIに聞いてみると、この組み合わせで奇妙な画像ができることは前から知られていて、アーティストの方々は使っているということでした。まあ、そらそうでしょう。
今回の話の中心となるディスプレイスメントは、Touchdesignerにもblenderにも備わっている技術で、簡単に言えばで色から凸凹を作る技術です。Touchdesignerではpbr(Physically Based Rendering)の中に含まれます。この技術を考察していく前に、その基本となる色によるベクトル計算の話を説明いたします。これは数の多いpointを扱う時に頻繁に使う重要なテクニックです。恐らくコンピュータ特有の計算方法だと思います。
位置を表すには(x, y, z)が必要です。x, y, zの値は本来どんな値でも使えますが、最大値を決めてx, y, zそれぞれ0~1の間にくるようにスケーリングします。一方色情報はR, G, Bで決まります。このR, G, Bのそれぞれの値は0~1の間です。この値によって様々な色が作れます。この色は平面で描くと、四角に色がついていることになります。このようにR, G,Bで三次元なのですが、色で表すと、色がついた四角というように2次元で表せれます。例えば100個の色が必要なら1×100の数の四角を並べてもいいし、10×10の100個の四角を並べてもいいですが、いずれも平面に並びます。これを利用するのです。つまり0~1にスケーリングした位置情報(x, y, z)を(R, G, B)に対応させるのです。つまり(1, 1, 1)の座標なら白として表せれるということです。この方法で、全ての座標は色に変換され、3次元位置情報は色をならべた2次元平面に変換されます。そうすると、位置A-Bのようなベクトル計算は色の平面の引き算として計算します。つまりベクトル計算が色でできます。そして何か計算した後のRGBが、位置(x, y, z)になっているわけです。形を構成するポイントが多いほど、この方法は格段に便利になります。これをつかわないと、x, y, zを表(table)にして、表計算をすることになります。もちろんできますが、簡単さが違います。
ディスプレイスメントというのはおよそこの変換を行う技術です。簡単な例では、平面を細かくメッシュ化します。そこへ色を適当に描きます。これにはいろんな色を使います。そうすると、その色に応じて、表面が凸凹になるということです。実際はもっと難しい計算をしていると思いますが、ディスプレイスメントの基本はこれです。色が形状に変換されるということです。
blenderのディスプレイスメントには2種類あります。一つはシェーディングと呼んでいる範疇で使うタイプと、モディファイアーと呼んでいる範疇で使うタイプです。シェーディングの中で使うタイプは、実際にメッシュを変更しません。見た目が凸凹になるようにみせる技術です。例えば、建物の絵が描いてある絵画の場合、キャンバスは平面なのに絵は立体に見えます。シェーディングはこれに相当する技術です。3D形状に変化はありませんが、見た目を3Dに見せるのです。一方モディファイアのディスプレイスメントは、3D形状のメッシュを変更して立体を作ります。上で上げた3つの図は、シェーディングの中で使ったディスプレイスメントです。実際のメッシュが変形しているわけではありません。この2つのディスプレイスメントの話は次回のブログで登場することになるでしょう。
ではなぜこのディスプレイスメントの操作が、予想外の形状を作り出すのかについて考察して行きましょう。上の図のような絵が描けるには、ボロノイテクスチャーとノイズテクスチャーとディスプレイスメントという色を位置に変換する操作でよく起こることを述べました。ボロノイテクスチャーというのは次のような模様のことです。

左は形状の表し方、右は色分布による表し方です。ボロノイのイメージはこの2つのどちらかだと思います。形としてのボロノイは、細胞のセルのような集まりの形です。セルの中央付近が持ち上がっていて、周りが低くなり細胞壁にあたる区切りがあります。色でいうと隣接したセルが色分けされています。総合してボロノイテクスチャーをカラーで描くと、

のようになります。細胞のように区切られていて色分布があるというのがボロノイです。色はセルの中央が強く、壁のほうが淡くなっています。セルの中の色分布は形を反映しています。これを見て、非線形性が潜んでいると思った方はいらっしゃいますでしょうか?壁があるということは関数でいうと、そこで曲がり、立ち上がっているということです。そして、セルの中でも中央が高く周りが低いということはこの部分はなめらかに変化する関数になっているはずです。これが連続しているのがボロノイテクスチャーです。この図形そのものに非線形性が含まれているのです。そしてディスプレイスメントする色の要素が入っています。推測すると、予測できないような形状を作る際にボロノイを使う場合が多いのは、セルの壁に対応する強い非線形性と緩やかな非線形性とを合わせ持っているからだと思います。
次にノイズテクスチャーの例を示します。
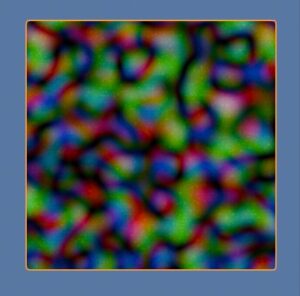
結構はっきり分かれております。明確な違いを連続して補間するのか、ステップ関数で補間するのかで随分違うとおもいますが、これを平面図形に適応すると、はっきりとした凸凹になるでしょう。しかしスケールを変えて近くまでよるとゆるやかなカーブになるわけで、どのようなスケールでノイズやボロノイを適用するかは重要です。いずれにしても、関数としてみると、非線形性が入っていることに気がつくでしょう。
ボロノイテクスチャーやノイズテクスチャーに非線形性が入っており、これが入力になります。この入力に対してこれを操作する部分、これがディスプレイスメントですが、ここに非線形性がなければ、単に重ね合わせた出力となり、意外性はでません。ディスプレイスメント自体にどうして非線形性が入るのでしょうか、これが次に考察することです。ここで生じる非線形性がパソコン内で発生する現象なのです。各ポイントは色情報をxyzに変換するわけですが、ポイントポイントとの間はどうするかというと補間します。なめらかにつながるように関数を使います。実際にどのような関数なのか知る由もありませんが、なめらかにつながるようにしていることからこの関数が非線形であることは明らかです。ノイズテクスチャとボロノイテクスチャの非線形性の複雑な形が、このディスプレイスメントの非線形の関数に入力され、予測がつかない複雑な形状を作り出すのです。コンピュータは全て論理で動いているので、不確定な要素は無いように思われますが、実はそんなことはなく、計算上で入ってくる非線形性によって「何だこれは」が生じることもあるのです。こうした現象を積極的に利用し、意外性を作っていくのです。
非線形性は意外性を作り予測できないわけですが、それはつまりコントロールができないということです。これでは工学になりません。そのままが美しく、これでいいと思う場合もありますが、何だこれは、で終わることもしばしばです。そこで、非線形性で現れたモノを加工して、人が推論できるようにしていきます。非線形性そのものは予測できませんが、パッケージして少しわかるようにする、ということが必要になります。ベイズ推定の話の時に、人は常に推定している、と述べました。この人の推定するという働きを刺激するというのが、インターラクションの目的です。あまりにも複雑でわけがわからない場合、人は推定せずに、もうわからない、私と関係ない、というように興味を失う傾向もあるように思います。この間を探ることが実際には重要です。非線形現象を扱う時は、このわからなさとコントロールとの間の妙が鍵でしょう。次回のブログではこの非線形性のわかなさをどうコントロールしていくのか、を考えていきましょう。
余談:コンピュータにはこのように補間するということから非線形性が生じます。しかし人間の視覚について思うと、「何だこれは」と思うような映像が次々と浮かんでくるということはありません。自然界を形状を関数にするなら、非線形性で満ちており、そして処理する視覚も補間しているでしょう。だのにこの違いはどういうことなのでしょうか。全く扱い方がコンピュータと違うのか、抑圧機構があるのか、ではないでしょうか。私はまったくわかりませんが、人が行っている処理と比較するのはおもしろそうです。



コメント