Boidsの説明
初期の人工生命の代表はおそらく、2次元セルオートマトンであるConway, 植物の成長シミュレーションとフラクタルを作るL-system、そして今回紹介するBoids(ボイドと読む)の3つでしょう。ConwayとL-systemは、このMonogokoroのblogで既に何度か取り上げてきました。今回はBoidsについて紹介致します。Boidsは多数の個体が群としての自然な行動をシミュレーションするプログラムで、レイノルズによって考案されました。鳥や魚の群れをシミュレーションするのが代表的で、現在は映画に頻繁に使われているCGの技法です。鳥のアンドロイドを意味する「birdoid」を縮じめて「boids」と呼ばれています。「boids」は3つの動作規則だけで動きます。オブジェクト同士がぶつからないように距離を取る(分離)、オブジェクトとオブジェクトが概ね同じ方向に動くように速度と方向を合わせる(整列)、オブジェクトが他のオブジェクトが集まっている群れの中心方向へ向かうように方向を変える(結合)、です。結果として鳥や魚の群れが実によくシミュレーションできます。応用はこれだけでなく、ぶつからないクルマのシミュレーションや建物等の情報を加えることで災害時の避難経路のシミュレーションに使われています。魚や鳥の群れのシミュレーションについては、YouTubeにすでに多くあるので、そちらを見てください。Touchdesignerにはscript SOPというpythonプログラムを書くオペレータがあります。それを使うと、boidsの本体のプログラムはpythonで書き、表示等の部分をビジュアルプロブラムを使うこともできます。また本体部分をGLSLで書くこともできます。余談ですが、AIを使うとpythonやGLSLは相当正確に生成してくれるようになりました。ビジュアルプログラムに対してはアドバイスをしてくれますが、Touchdesignerのプログラムを書いて提供してくれるまでには至っていません。歴史あるプログラムはpythonやGLSLをAIによって生成させる方法も便利な手法だと思います。
Boidsの動きとプログラムの説明
今回説明するのは、先に2回続けてアップした「擾乱を伴う反復系」の線状の束に鳥や魚に相当するオブジェクトをインスタンシングし、boidsと同様な動きを作ろうとするプログラムです。上の3つの動作規則に「擾乱を伴う反復系」が加わるので、制御性や拡張性が上がります。pythonやGLSLを使う方法もあるかと思いますが、全てビジュアルプログラムで記述しています。先のblog「ポストモダン・・・2」の最後の動画を見てください。この細胞のような形の動画は、すでに群コントロールと言えるでしょう。しかしこの場合、細胞同士はぶつかっています。重なりをよしとして描いています。また円形状の形ですので、どちらが前ということがありません。これに対して「boids」としてふるまうようにしようとすると、衝突を回避する必要と、頭の向きが進行方向にそろっている、の2つの点を加えなければなりません。Touchdesignerで衝突回避するプログラムが、https://www.youtube.com/watch?v=TVErfVWqYpU&t=14s にありましたので、これを参考にして「擾乱を伴う反復系」に適用しました。この方法は、前のblog「コンピュータに宿る非線形性、ディスプレイスメント」で少し述べた座標を色で表す方法を使っています。座標を表す(x, y, z)を最大1最小0にノーマライズすると、色情報である(R, G, B)として表すことができます。こうすることで、3次元の位置がRGBの値で設定した一つの色で表せます。そうすると、色を足したり引いたりする演算によって、位置のベクトルが計算できます。非常に頭のいい計算方法です。今回もこの方法を使います。
それではまず、動画を見ていただきましょう。
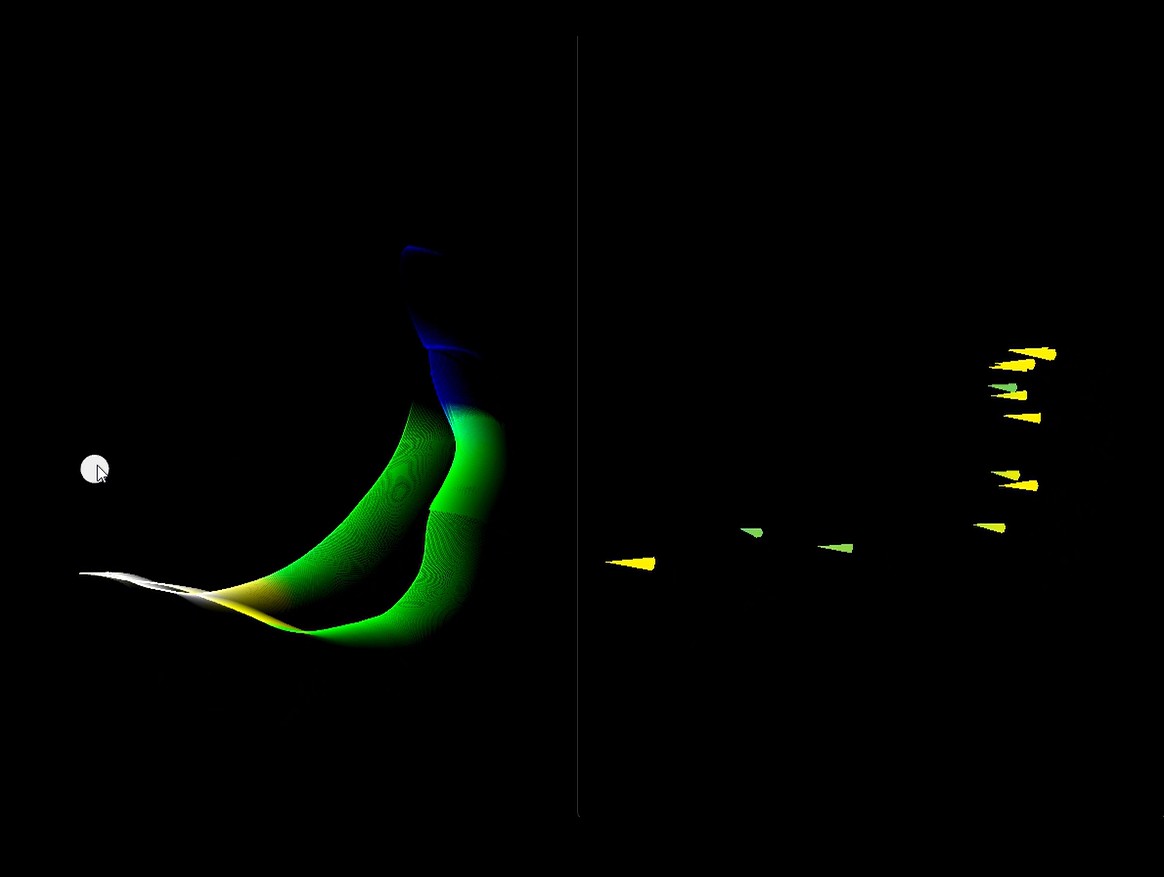
左側の図が「擾乱を伴う反復系」の線状の束が、マウスに向かって移動する図です。線状の束から13ポイントを選んで円錐の形状をインスタンシングしたのが右の図です。この時に、上述した3つの動作規則が加味されています。カメラの位置によって2次元平面的に見せていますが、boidsは3次元空間を動いています。重なっているように見える部分もありませすが、奥行き方向にずれています。もう一つ動画を見ていただきます。
この動画は、線状の束を作るspring SOPのパラメータdragの値を1から3に変更した場合です。dragパラメータはポイントの動きに対する抵抗力を表しています。この値を大きくすると、ポイントが動こうとしてもその動きが抑えられます。つまりforceで動かそうとしても広がりにくくすることができるため、群の広がりを抑制することができます。「擾乱を伴う反復系」利用して作製したBoidsは、従来のBoidsより制御性が上がっています。
次にプログラムについて説明致します。次の図が衝突回避部分のブロック図です。
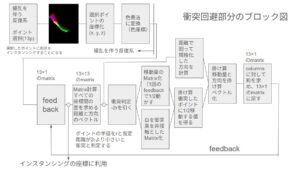
擾乱を伴う反復系と書いた矢印がありますが、それ以降が衝突回避部分です。そしてfeedbackと書いた部分からインスタンシングの座標に利用と書いた部分に矢印があります。これが衝突回避部分からの出力になります。この座標に対して円錐の図形をインスタインシングすると上の動画となります。やっていることは、線状の束から選択したポイント13に対して、他のポイントが衝突しているかどうかを判定し、衝突しておれば、衝突の反対方向に少しずらす、ということをフィードバックを使って繰り返し行い、衝突したポイントを動かしています。13ポイントの位置は13×1の色マトリクスに変換して表します。1つのポイントは(x, y, z)なわけですがこれが(R, G,B)に変換しているので、一つのポイントの位置は青とか赤とか色で表されます。これが13ならんだのが、色マトリクスです。更に他との衝突を求めるために、13×13の色マトリクスを作ります。自分と自分を含む他のポイントとの関係をこのマトリクスで表せます。ポイントに想定した大きさの半径をrとすると、2rより小さいと衝突していることになるので、これを引いて衝突判定を行います。そしてそれを、衝突判定を表す白黒のマトリクスにします。一方で移動させる距離を設定し、大きさと方向を計算します。方向は衝突の反対側に動きます。方向は衝突距離で割ることで方向ベクトルを作っています。移動する値と方向をfeedbackして衝突を回避します。この衝突を回避するブロック図は自分でも考えれると思いますが、だからといってプログラムがかけるわけではありません。上記のYouTubeのおかげです。
実は擾乱を伴う反復系を含む全体のプログラムは正確とは言えません。それは線状の束と独立して衝突回避処理をしているからです。本来なら衝突回避した座標は線状の束の座標に反映されるように、フィードバックする必要があります。これをまともに考えると「擾乱を伴う反復系」の外側にもう一つのフィードバックが入る系になります。一般的には2重のフィードバックは安定させるのが難しくなります。別の方法を考えたほうがいいような気がします。今回は何もしていません。
上の動画を見ていただくと、マウスを追っかけて円錐が動きます。そこに障害物を入れてそれを回避させるにはどうすればいいだろうか、また動く場所を制限して、出口に誘導するにはどうすればいいだろうか等、環境を入れてみるとどうなるだろうと思われるでしょう。実際こうしたことが検討されて行きます。例えば災害時に建物内に複数の人がいる場合に、どういう避難の経路を進むのか、といったシミュレーションです。このような拡張性のためには、本来のBoidsに何かプラスした機構が必要です。今回の場合だとそれが「擾乱を伴う反復系」になります。環境の変化を加えた場合を近々紹介したいと思っています。


コメント