Monogokoroのサイトでは、予測不可能な振る舞いを創発につなげようとしています。このため、フラクタルやカオス、blenderで生じる非線形現象、擾乱を伴う反復系、と非線形性に力を入れて述べてきました。これからもそのつもりです。しかし予測不可能性は線形操作でも現れます。この現象も将来創発に活用できるのではないかと思っています。そこで線形操作で生じる予測不可能性について考察致します。これは人の認知とも関係していると思います。かならずしも操作の数学的性質だけではないでしょう。先のblog「人とモノとの間・・・」では、感覚が「人とモノとの間」にあり主客未分である場合を議論しました。今回はその例でもあると思います。それでは解説する動画をまず見ていただきましょう。
この動画を見ると、顕微鏡か写真で放散虫や紡錘虫を見て描いたか、あるいは非線形性を利用して偶然できた形なのではないか、と思われたでしょう。しかしそうではありません、これは単純な図形のコピーとインスタンシング(インスタンシングはある図形を別の図形やパーティクルのポイント全てに割り付ける操作です。各ポイントにいっぺんにコピーする操作と似ています。ただインスタンシングでは、コピーと違って貼り付ける図形をランダムにサイズを変えたり回転させたりできます)から作製しています。コピーもインスタンシングも線形な操作です(線形代数を使ってできる操作が線形です。つまり移動や回転、スケール変更等のことです)。動画は図形をコピーとインスタンシングで作って、真下から見た図形です。人は単純な図形を重ねて、それを下から見た図を想像する場合、立方体の角に三角錐を付けて下から見てみたというようなことですが、これぐらが想像できる限界ではないでしょうか。立方体が複雑な多面体になり、そのポイントに三角錐をつけた図形を下から見た際どうなるかとなると、もはや想像できないでしょう。つまり人の図形の組み合わせに対する認知は直ぐに限界になり予測できなくなります。これは図形が複雑になるということはもちろんありますが、人の認知能力の性質ではないかと思います。進化の過程でそんなに必要性がなかったのでしょう。私見ですが、人は構造よりも輪郭を認識するように発達したように思います。こうした性質を利用すると、何だこの図形はという予測不可能な図形や模様を次々と作り出すことができます。造形や文様の作製には活用できると思います。また先に放散虫や紡錘虫を挙げましたが、自然が作る形状に似た形状になる場合がしばしばあります。これは自然がある形のコピーの組み合わせでその姿を作っているのではないかという印象を与えます。次の動画は上の図形を斜め上から見た場合の立体図形です。この図形の真下から見たのが先の動画でした。
なかなかカッコイイ形状ではないでしょうか。このような形状を元の図形から想像することは、直ぐ後にプログラムの主要部分の説明をしますが、ある程度できます。しかしそれを真下から見るとどうかと言うとく予測できません。この現象に少し似ていると思うのが結晶構造です。原子が規則正しく配置しているのですが、少し複雑な結晶構造の場合、立体模型を少し斜めにしただけで、とても複雑に感じたり、全く違うモノに見えます。それでは図を使ってプログラムについて簡単に説明致します。次にプログラムの主要部分を示します。Touchdesignerによるものです。
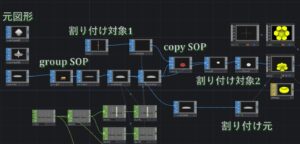
元図形が基本となる図形です。group SOPで使う部分を選択します。使わない部分は次のdelete SOPで除きます。この図では元図形の上半分を使いました。この図形のポイントに、割り付け対象1の細い立方体を割り付けます(動画ではヒゲのように見えるのがこの図形です)。この操作がcopy SOPです。この時点の図形は想像できます。次にインスタンシング部分の拡大図を示します。
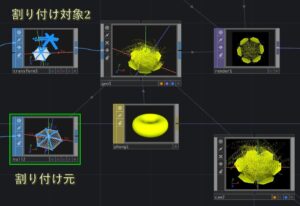
copy SOPした図形(割り付け対象2)を、割り付け元と書いた元図形の上半分をスケーリングした図形の各ポイントに割り付けます。これはインスタンシングによって行います。これも完全とはいえませんがある程度想像できるでしょう。こうしてできた図形を真下から見たのが最初の動画です。これは実行して初めて形がわかります。非線形性を利用する場合は、元の形が線形代数による変換と異なる形になって現れるので予測できないわけですが、今回の操作は図形の形状が変わっているわけではありません。複雑だと言う事と視点が違うという事、重なりあっているという事、で事実上予測不可能になります。割り付け元を見ていただくと、6角形になっています。これは元図形のsphere SOPのパラメータであるRowsが23, Columnsが6のとなっており、Columnsの数を反映しています。試しにColumnsが3の場合の動画を次に示します。
三角形が基本配置になっていることが分かります、Coulumsの数を多くしていくとどうなるでしょうか、こうして作製したのが、前のblog「オブジェクト指向プログラム、世界の捉え方」で描いた古代の鏡の図になります。すなわち円形になっていきます。
それでは、もう一つ例を挙げておきます。
線形動作から予測不可能性が現れること自体興味深い現象です。非線形の場合も同様ですが、全てが予測不可能であれは設計になりません。構造等は設計で迫れるが、最後は予測不可能になるというのが丁度良いのです。今回の図形は、模様の作製や物の空間配置の参考に、また生物の形状や成長を模倣するのに役立つと思っています。


コメント