先に人工生命の有名な例としてConwayを紹介しました。今回はこれも初期の人工生命の代表であるL-sysytemについて説明します。L-systemは植物の形状や成長をシミュレーションするのに現在も頻繁に使われています。これはリンデンバウワーという方が発明されたので、その頭文字をとって、L-systemと呼ばれています。今回は植物の幹や枝に相当する部分の話をします。しかし植物の形状を作るには葉や花や実も作る必要があります。これらは別のプログラムブロックとして作製し、L-systemと合わせて植物を作製します。幹や枝が成長するにつれて、葉や花も成長し、枝の特定のところから葉や花が付き、また咲く必要があります。このように、幹や枝と葉や花は連動して動く必要があります。このようにするためには、それぞれに関係性を持たさなければなりません。このようにA,B,C ・・・を作って、それぞれが関係性を持って動かす技術をプロシージャルと言います。このプロシージャルはプログラムにしてもハードウエアにしても、極めて重要な技術で工夫のしどころです。プロシージャルは仏教でいう縁起のような関係だと思います。これについては日を改めて扱うつもりです。植物のシミュレーションについていうなTouchdesignerのL-systemは、葉や花との関係性(プロシージャル)をつけやすいオブジェクトになっていて大変便利です。TouchdesignerはL-systemが得意なプログラムだと感じます。
今回L-sysytemを説明するのですが、その中心概念に「再帰」があります。再帰は、L-system,フラクタル, フィボナッチといった、自然のふるまいと関係するような現象に登場する共通の概念で、自然的な何かを工学に取り入れようと思う場合に必須です。L-systemは再帰を理解するための例としてとても役立ちます。再帰というのは次のようなことです。在る構造Aを作っておいて、その構造Aを操作して何かにつけたモノが次の構造になる。そしてその構造は、A+何かに、更にAをつけたもの、といったように、構造Aがどの世代にも付け加わっていく構造のことです。これは普段に使う、y=f(x)のように、独立変数xによってyが決まるという関係とは全く違っています。自分自身を前の自分自身が規定する関数です。どうやら自然は構造を再利用していて、同じ構造を使って成長させている側面があるようです。再帰を使ったL-systemやフラクタルやフィボナッチの形に人は魅力を感じることが多いようです。何故人は再帰的な現象に美しさを感じたり魅かれたりするのかはわかっていません。自然は再帰性を利用しているし、人も再帰性を利用しているという共通性があるからなのかもしれません。ユクスキュルの「生物から見た世界」を訳され、環世界という概念を日本に紹介された日高敏隆さんなら次のように言われるかもしれません(勝手な想像です)。「生物や植物や人の中には再帰が使われている。もし人が再帰を利用した構造が嫌いであったなら、外へ出て植物を取ったり食べたり、育てたり、また建物を建てたりして暮らすことはできなかったでしょう。今人類が生き反映しているということは、人は再帰現象が好きだからです。再帰現象が好きになるように進化してきたのです」なんて。私は人とモノとのフォードバック、コミュニケーションに関心があるので、再帰の概念を利用したモノが、人との親和性が高くなるのではないかと思っています(仮説です)。L-systemやフラクタルを活用してモノを作製している理由はここにあります。つまり再帰を使ったモノは人もまた再帰の特質を持っているので、響き合うところがあるのではないかというわけです。この考えは、先回述べた「思弁的」という態度です。
L-system
さて前置きはこれくらいにして、L-systemについて考えていきます。これは再帰の理解にもなります。
植物の例
下図にL-sysytemで描く植物の例を示します。
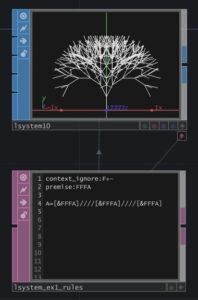
この図を理解することが今回の最初の目標です。下段にpremise:FFFA A=[&FFFA]////[&FFFA]///[&FFFA]と書いてありますが、これが上の木の式です。相当にシンプルです。この記号を理解することで再帰性も理解できます。最初によりシンプルな例からはじめてみましょう。少々めんどくさいですが、ゆっくり追いかけていってください。
priemise:A, A=F+AFの例です。premiseは全体の基本構造、Aは再帰の構造を現しています。第1世代の図が次になります。
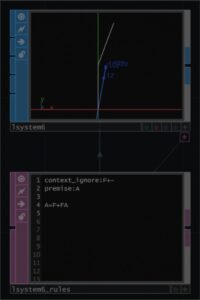
Fは上に1伸びるという意味です。従って一回目はF上に1伸びて、+はx方向に曲がるという意味です。足し算とは違います。その角度は指定することができ、この例では20°にしています。この曲がった状態で、Fで1伸びる。この結果を示しています。右辺の最後のAは前の世代のAを現していますが、前の世代はないので付け足す記号はありません。ですので、第1世代のAは A=F+Fになっています。
次に第2世代を考えてみます。
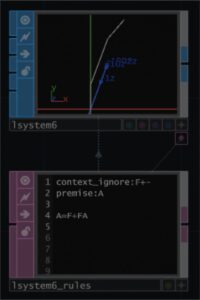
A=F+FAの右のAは第1世代のAのことです。ですのでF+Fのことです。従ってA=F+FAは、AにF+Fを代入して、A=F+FF+Fとなります。図でいうと、第1世代のF+Fの終わったところから、前のAが追加されるということです。これが上の図です。この前の状態を利用するのが再帰です。
次に第3世代を考えてみます。
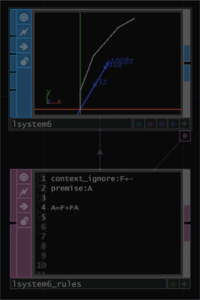
A=F+FAの右辺のAは第2世代のAのことです。すなわちA=F+FF+Fのことです。従って、A=F+FF+FF+Fとなります。図でいうと、第2世代の先にF+Fが追加されたことになります。
次に、世代を繰り返して第8世代の図を示します。
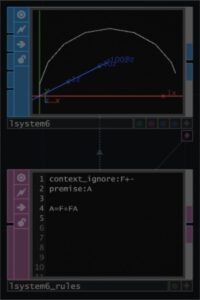
A=F+FAのAは第7世代のAが足されたものとなっているわけです。
この例で、およそ再帰という意味がつかめたかと思います。在る構造を作っておいて、それを追加していく方法なのです。
それでは、最初に上げた。premise:FFFA A=[&FFFA]////[&FFFA]///[&FFFA]の例に挑戦してみましょう。
今度は、全体の基本構造はFFFAとなっています。再帰が働くのはAの部分なので、まっすく3回伸びた後に再帰されていくという構造になっています。再帰の構造がA=[&FFFA]////[&FFFA]///[&FFFA]です。次に第1世代の形状を示します。
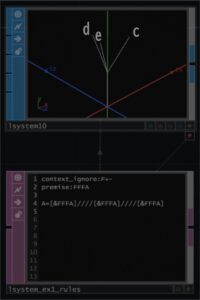
Aの右辺には[ ]があります。これは[ ]の中の処理をして処理前の位置に戻るという記号です。&は+と同様曲げですが、Z軸方向に曲がる記号です。設定により30°曲がるようにしています。その後FFFですから3回連続して伸びます。次に再帰のAが入っています。しかし1回目の前は何もないので、。最初に使う時には右辺のAは付け足すモノはありません。[ ]のカッコが閉じるので、元の位置に戻ります。元の位置というのはFFFした最後の位置になります。次に/があります。これは反時計周りに回転する記号です。30°に設定してあるので連続4回で120°回転します。そしてそこから、[ ]の中の操作がはじまります。これは先ほどと同じ操作です。そして元の位置に戻る。その後120°ずれてもう一度行う。これがAの操作ということです。従って図のように三又の図が描けることになります。
次に第2世代の図を示します。
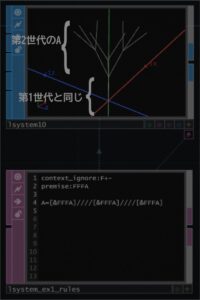
A=[&FFFA]////[&FFFA]///[&FFFA]のAのところが、第1世代のAですので、これを代入すると、
A=[&FFF[&FFF]////[&FFF]////[&FFF]]////[&FFF[&FFF]////[&FFF]////[&FFF]]////[&FFF[&FFF]////[&FFF]////[&FFF]]となります。もう第2世代から再帰的な表示にしないと、実際に書いていくのは非常に手間がかかります。A=[&FFFA]////[&FFFA]///[&FFFA]の右辺のAの位置に注目してください。再帰が発動するのは&FFFと進んだ後だということです。これが120°ずれて3回あるわけですので、構造が追加されるのは、第1世代の図のc, d, eの位置からだというわけです。ここから、A=[&FFF]////[&FFF]///[&FFF]の三又の形状が付け加えられます。
次に第3世代の図を示します。
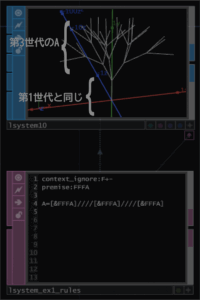
第2世代はA=[&FFFA]////[&FFFA]///[&FFFA]のAのところが第2世代のAということなので、A=[&FFF[&FFF]////[&FFF]////[&FFF]]////[&FFF[&FFF]////[&FFF]////[&FFF]]////[&FFF[&FFF]////[&FFF]////[&FFF]]を代入すれば求まります。もうやめておきます。再帰の記載方法がいかに効果的か、自分で追って行くと実感することができるでしょう。図の解釈でいうと、第2世代の&FFFの後に三又の構造が付け加わることになるわけですから、9個ある&FFFに三又の構造を加えることになります。premiseはFFFAですので、FFFの上が再帰されていることに注意してくだい。FFFは変化していません。
ここでは簡単な例を行いましたが、L-systemは多数の処理記号を持ち、また植物によってはその構造も非常に複雑なものがあります。「Przemyslaw Prusinkiewicz Aristid Lindenmayer The Algorithmic Beauty of Plants」という文献には、非常に多くのL-systemの例が紹介されています。複雑なパターンはこうした文献を見て例を作り、それを変形していくというのが実際だと思います。想像して式がかけるという範囲は極簡単なモノに限られます。
フラクタル
さて、このL-systemはフラクタルも書くことができます。フラクタルは自己相似性を持つ幾何学構造のことです。自己相似性を特徴としていることからして、同じ形状を繰り返すわけですから、再帰を使うということは想像できるでしょう。しかし、再帰の仕方が植物の場合と違っているのです。結論からいうと、自分自身全体を再帰する。これがフラクタルです。植物の場合は、自分自身の中の特定の部分を再帰しており、自分自身全部を再帰しているわけではありません。以下によく知られたフラクタルの例を考えてみます。これを知ることで、植物とフラクタルの違いがよくわかると思います。
コッホ曲線の例
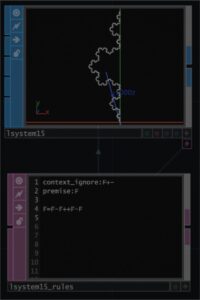
上の図がコッポ曲線です。この図は第8世代です。premise:F F=F-F++F-F たったこれだけで描けます。植物と大きく違っているのは、全体の構造を表すpremaiseもFで、そして式の右辺が回転はありますが、全てFで書かれている点です。F-F++F-Fの操作した図形が、次の世代のFになるわけで、前の世代に作った自分自身が次の世代の自分自身のそれぞれの部分になるということです。これが自己相似性なのです。実際に描いてみるとすぐわかります。第1世代から見ていきましょう。
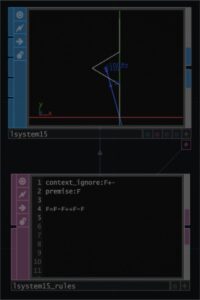
第1世代はF-F++F-Fですから、上に進んで、-記号、これは+の逆で-x方向に曲がります。曲がる角度は60°に設定しています。ですので、マイナス方向に60°曲がってFで進みます。次に++ですがからx方向に120°曲がります。そいてFで進みます。次に-60°もどります。図ではy軸上にきます。そしてFで進みます。
次が第2世代の図のです。
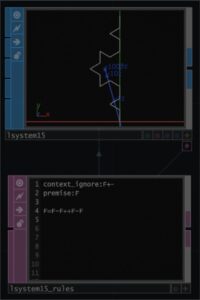
F-F++F-Fが第1世代のFですので、 F=F-F++F-Fの右辺のFにこれを代入したのが第2世代のFとなります。図形としてはFの伸びるところに、第1世代の形状が代入されることになります。
これを繰り返すと、第8世代では最初に示した図になります。
シィエルピンスキーのギャスケットの例
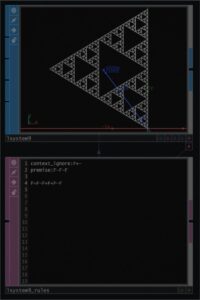
上の図はシィエルピンスキーのギャスケットと呼ばれているフラクタルである。第5世代を記載している。これについて考えてみましょう。
premise: F-F-F F=F-F+F+F-Fがその式です。回転角度は120°です。premiseがF-F-Fとなっているところに特徴がみれます。premiseは全体の構成ですから、F=F-F+F+F-Fの図形を描いて、それをそのまま、-120°回転して置く、さらにー120°回転して置くということです。同じ形のものを回転して3つ配置することがわかります。その配置するモノはなにかというと、F=F-F+F+F-Fできまる形だというわけです。それではF=F-F+F+F-Fの形をみてみましょう。これまでのように順次おっていくと次の形になります。
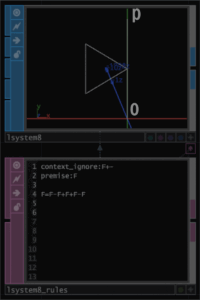
y軸と重なっているところがあって少し見にくいですが、Fの直線があって三角形があって、更に直線がついています。ここで重要なのが終点です。この式の終点をpとしています。premiseの-Fの意味はこれを-120°ずらした形を加えるという意味です。この図と同じ図をpから真上に書いて、それを-120°回転させると思うとわかりやすいかもしれません。そしてその終点から、さらにこの図形を書いて-120°形をずらして加えたものが、第1世代になります。ですから第1世代は次の図ようになります。
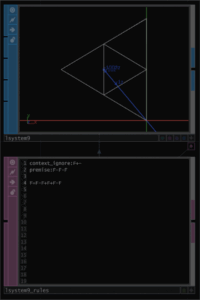
premiseのF-F-Fを行った場合の最終点はどこかというと、oに戻ってきていいます。
第2世代は次のようになります。
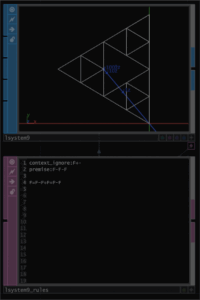
第2世代はF=F-F+F+F-Fの右辺のFのところが、第1世代の形状に一つ一つ置き換え、その置き換えたものを、こんどはF-F-Fに配置するという、手で行うと相当厄介なことをしています。それを行うとこの図になるということです。形を構成する線の一本一本は何度か重なっています。
第3世代は次の図形になります。
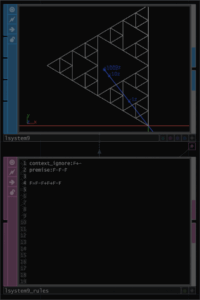
これは第2世代の図形をF=F-F+F+F-Fの右辺のFのところに入れて描いた図を、F-F-Fに配置した図になります。もはや手では追っていけません。しかしL-systemを使うとわけなくできることになります。再帰というのは、本当に強力でコンピュータに適した方法です。これを書いていて思ったのですが、この書き方は線の重なりが相当にあります。式を工夫するともっと少ない重なりで書けるかもしれません。
簡単な例しかしておりませんが、再帰の重要性とL-systemの強力さ、そして植物を扱う場合とフラクタルとの違いとが理解できたのではないかと思います。最初に述べたように植物をあらわすには葉っぱや花との関係をつけるプロシージャルが必要ですが、Touchdesignerはそこも便利です。植物が成長し葉や花をつける例を作製したのでそれを次に示します。
また、L-systemを使っていると、実際にはない植物がつくれます。作製した例を次に示します。

アマゾンの奥地でひょっとしたらこんな植物が発見されるかもしれません。
今回の記事の表紙にした実がなって胞子を飛ばしている絵ですが、これもL-systemで作製した架空の植物です。このような非常に複雑な形状を描くこともできます。
L-systemについては、https://www.youtube.com/watch?v=h6U-RVpG5X8
がとても参考になります。これを作製されたAkiko Yamashita様はL-systemに関するYoutubeを複数上げておられます。
フラクタルを作製するもう一つの方法
述べてきたようにフラクタルは一つ前の自分自身をコピーしてそれをそのまま次の世代の部分に当てはめます。このことから前の自分自身をコピーあるいは少しずらして、部分に戻すことでフラクタルができそうです。つまり、フラクタルはL-systemを使わずにフィードバック系を用いて作製することもできるということです。これもまた、プログラムならではの画期的な方法と思います。Touchdesingerでは、フィードパックを行うためのfeedback TOPという特別なオブジェクトが用意されており、これを使うことで作製できます。この方法で作製したフラクタルの例を次に示しておきます。うねうねと動いているのは人工生命を入力に加えているためです。このようにフラクタルの変化の中に動きを入れることもできます。
フィードバックを使ってフラクタルを作製する方法は以下が参考になります。
「https://www.youtube.com/watch?v=h6U-RVpG5X8」
可能性について
L-systemの最後に新しい可能性について述べておきます。L-systemに対して外部から、あるいは第n世代の結果を処理して、第1世代の形状にフィードバックできたら、L-systemは非常に大きく変容するでしょう。規則的な進化ではなく、思いもよらない進化の可能性を示せるでしょう。これは創発に直接つながります。残念ながら、市販のソフトでは動的にL-systemは動かせません。世代は動かすことができるのですが、しかし研究はされているようで進展が楽しみです。
フィボナッチ数列
L-systemとフラクタルの話で終わってもよいところですが、自然を模倣する技術をモノに適応して人との親和性を高めようと思っている私にとって、原点的なフィボナッチ数列に触れないわけにはいかないでしょう。フィボナッチ数列自体はインターネットに多くの記事があるので、私からはフィロタキシスとの関係を述べて、若い時に「なんなんだこれは」と、感激した話を加えておきます。下図はフィボナッチ数列をまとめたものです。

漸化式F(n) = F(n-1)+F(n-2)が前の値とその前の値で今の値が決まることを述べており、再帰を示した式です。自然の中にこの関係の数列が多くみられること自体が驚きです。多くの人にとって、再帰が自然と関係してると思った原点がこの式ではなかったかと思います。そして、一般項にでてくる。
(1+sqr(5))/2が、黄金比、黄金角となって、人が感じる美しさとも関係しているのです。再帰、自然、美とをフィボナッチは結びつけています。下の図は、0,1,1,2,3,5・・・の数列の値を、正方形の辺の長さにして描かせた有名な螺旋の図です。
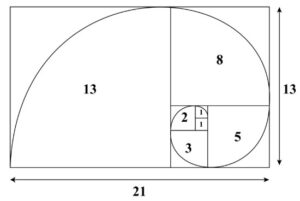
この図をみると。辺の値が、2:3の四角形、3:5の四角形、5:8・・・の四角形等がでてきます。こられの比は、1.5, 1.66, 1.6・・・となっており、おおきな四角形では1.618・・・に非常に近い値になります。この値は、フィボナッチの一般項の(1+sqr(5))/2 = 1.618・・・と一致するのです。これが黄金比です。美しいと言われている比率が、フィボナッチ数列からでてくるのです。
フィロタキシス
植物の葉っぱの配置、ひまわりの種の並びから、松ぼっく鱗片の並び方がフィロタキシスになっていると言われています。フィロタキシスをまとめると次の図になります。

r=c・sqr(n), Φ=n×137.5°をTouchdesignerで描かせてみると、次の図ができます。

確かに、ひまわりに種の部分はこんな感じです。ここでこの2つの式はnの関数で、これだけでは再帰とは関係ありません。しかしこの137.5°がマジックナンバーなのです。一つ上の図に示したように、円周を1:(1+sqr(5))/2に分ける角度が137.5°なのです。これを黄金角といいます。ここに、フィボナッチ数列にでてくる(1+sqr(5))/2が登場しているのです。このことから、r=c・sqr(n), Φ=n×137.5°は再帰の式ではないですが、再帰と関係しているのではないか?ということなのです。具体的にどんな関係があるのかということは、今も分かっていないのではないかと思います。若い時に「何だこの関係は」と驚いたのを覚えています。そして、こうして今ブログを書いているこの時も、同様な感激を覚えます。
計算の上では、137.5°を別の値に変えても図か書けます。例えば132°にした時の図が次です。

この図に意味があるかどうかは別にして、結構かっこいいのではないでしょうか。文様としては活用できるように思います。
付け足しのコメント
人を含む自然の中にはほんとうに多くの再帰が入っています。そして、人は植物やフラクタル、フィボナッチ、フィロタキシスの描く形状に美を感じるのです。つまりモノと感性が結びついているのです。ここに最初に述べてように、この再帰現象をモノに取り入れると、人とモノとの親和性が上がるのであはないか、そういう仮説がでてくるのです。そして最後に再帰について別の見方を述べます。フィボナッチ数列にしても、L-systemでてきる形の座標にしても、これを並べると非線形になります。フラクタルを語るときこの非線形で語る場合が多くあります。このように、非線形の観点から再帰を捉えるのも興味深いアプローチのように思えます。非線形のほうが再帰よりも広い概念です。



コメント