カオス | Monogokoro

これまで、コンピュータに宿る非線形性やフラクタルについて述べてきました。今回は非線形性のもう一つの代表であるカオスについて述べます。カオスはフラクタルと同様に非線形で再帰的な現象です（再帰的というのは、前の状態で今の状態が決まるということです。例えば、x_n+1=ax_n(1-xn), F(n)=F(n-1)+F(n-2)です。「「再帰」とは、L-system・・・」を参照）。再帰的な現象はかならず非線形であるわけではありません。例えばx(n+1)=ax(n)+1も再帰方程式ですが線形です。
初期値が与えられるとその後の状態が決まることを決定論的と言います。ニュートンの運動方程式がその典型例です。カオスの特徴は、決定論的でありながら、初期値の僅かな違いが時間が経つと大きな違いになり、予測がつかないことです。これは次のようなことです。カオスも決定論ですから、厳密に同じ入力を入れると（無限の桁数まで同じ値を入れると）決まった出力が得られます。しかし実世界では同じと思っていても少し違うわけで、その違いによって出力が大きく変わります。これを予測困難と言っています。通常入力が僅かにずれると、出力もずれますが、そのずれ方は予測できます。しかしカオスはこの僅かな違いによって大きく異なる値となるので、入力をどれだけ正確にしても、無限の桁数で合わせることはできませんから、出力は予測できなくなります。これは数学と物理のギャップをぐなぐ領域です。通常数学的に求めて、実験で物理現象にそれを当てはめます。その時に同じ初期値にしたと思っていても、実際の実験ではある桁数では違っています。それが思わぬ結果になってしまいます。この予測困難がカオスのスリリングな特徴です。
こんな現象ってあるの、と思われるかもしれませんが意外に複数あります。例えば天気の移り変わりです。私は名古屋に住んでいますが、名古屋の天気を何年も記録しておくと、およそ周期的で何月ごろに雨が多いとかがわかるでしょう。しかし重要なのは、明日雨か降るかどうか、いつ雨が降るかです。だいたい梅雨には雨が多いですが、いつなのかは明確でありません。こうした現象はたいていがカオス的です。電力需要も、昼は多くて夜は少なく基本周期的です。しかし今日の10時はどうだろうとなると、正確な予測が難しいのです。交通量もこの傾向があります。こうした本来カオス的性質を持っている現象を予測するのに、カオスを使ったモデルを使うのは自然だと思います。カオスは決定論ですが、初期値が僅かに違うと、離れた時間では大きく値がずれることになるので、長期的な予測は難しいと言われています。工学的な応用としては、暗号やセキュリティ分野は勿論、もともと周期的な挙動が正常である装置が、非常に小さいがカオス的なふるまいが生じるような場合（またはその逆）に、異常の兆候として見つけるのに利用できます。また、数値解析では局所解に陥り最適解が探せない場合がありますが、常に変化する性質を利用して、最適解を探すのに利用する等も検討されているようです。

パイこね変換

カオスで最初に学ぶのは「パイこね変換」だと思います。これは非常に示唆的でおよそカオスのイメージを持つことができます。インターネットで検索すると多くでてきますが、重要と思う点を指摘したいと思います。次の図はパイをこねる操作を示した図です。

(a)はパイの生地です。青い部分に小さく黒丸をつけています。この位置がこねるとどこへいくかを問題にします。今回はx軸つまり、横方向の位置だけを問題にします。パイのこね方は、(a)を横方向に2倍して、半分を折り返します。これが(b)図です。結果(c)図が得られます。これを何度も何度も繰り返すと、黒点のx軸上の位置はどこにいくのかということです。これを図示したのが次の図です。

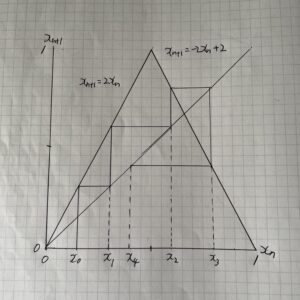
０～1が最初の図のパイの横軸です。2倍に伸ばしてから折り返して折りたたむので、計算式は、

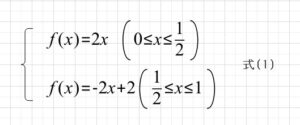
となります。図にはx_n+1=x_nも記載しています。これは作図するときの重要な線です。黒点の初期値をx₀とすると、x_n+1=2x_nに従って、x_n+1が求まります。このx_n+1の値がx_nとなって計算していくので、x軸に移す必要があります。これがx_n+1=x_nの直線です。x₁で２x_nは0.5を超えるのでx_n+1=-2x_n+2に移ります。x₃では0.5以下になるので、x₄は0.5以下に下がっていることが分かります。これを繰り返し行います。図3に初期値x₀=0.1の時とx₀=0.1005と僅かにずらした時のx_nの位置を示します。

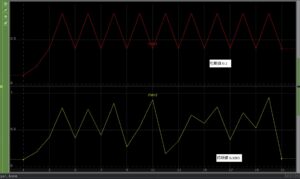
初期値0.1の時は、0.4と0.8との周期になりますが、僅かに初期値を変えた0.1005の時はばらばらになります。このばらばらさがカオスです。この僅かの違いて、性質が変わっているのは驚きです。カオスだと言うためには判定基準がありますが、これについては今回は省略致します。このグラフを見ると、基本的には凸凹していて周期ぽいわけですが、初期値が少し違うので、次々と変化した値が発生しています。今回の場合はｘ軸しかないので、いったん同じ値になれば、0.4と0.8のように繰り返しになります。繰り返しにならないのは、常に異なる値になっているからです。パイに付けた黒点は無限の桁まで同じ位置だと（つまり0.100000・・・とずっと同じ、数学的にはできることです）、決定論ですから0.4と0.8のように繰り返しの値になるわけですが、実際に印をつける場合はそうはできないですから、パイこねをしていくと、n回目にどこにいくのかはわからなくなります。しかし何の規則もなくばらばらかというとそうではありません。その値は、上の式(1)のどこかにはあるのです。この規則と不規則の間がカオスです。

ロジステック写像

次にロジステック写像の例を見てみましょう。結論からいうとこれはパイこね変換と非常に似たことになります。ロジスティックと言う言葉は物流のようなイメージを持ちますがそれとは関係ありません。人口や生物の数の変化の数学的モデルがロジステック関数です。論理的な推論や計算のことをロジックと言いますが、これから派生しています。
人口をNとするとその割合dN/dtは人口に比例するとすると、

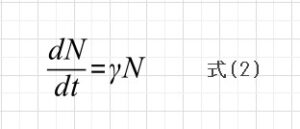
となって、

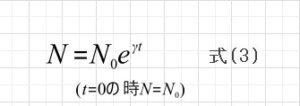
と解けます。

γがゼロなら増減はないし、正なら指数関数的に増え、負なら指数関数的に減ります。増える場合は、際限なく増えていきます。しかし実際はそんなことはありません。ほとんどの実際の現象の場合、ある程度増えたらその増え方は鈍化して飽和していきます。そこで飽和した時の人口をＫとすると　

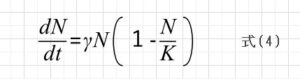
として、飽和するようにします（N=Kの時、dN/dt = 0となる工夫です）。
これを解くと

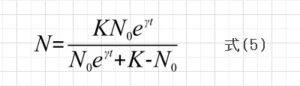
となります。これがロジステック関数です。これを図示すると

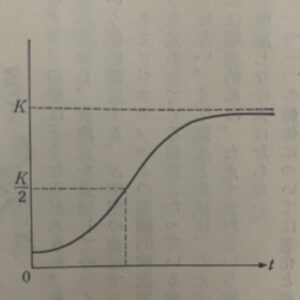
になります(ブルーパックスB-625　カオスとフラクタル　著者　山口昌哉）。
ここから更に難しくなりますが、上の本を参考にして結論だけいうと、

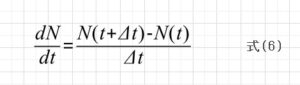
をとして近似差分法方程式にして、

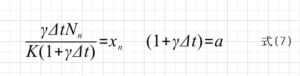
とすると、ようやく求めたい、ロジステック写像の式

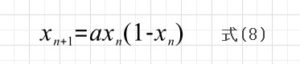
が得られます。これは前の状態x_nで、次の状態x_n+1が決まるので再帰の式です。
このx_n+1は何を表しているのかと言うと、次の世代における人口の割合を表しています。そしてaは繁殖率に相当し、成長の速さを決定します。aの値が高いほど繁殖率が大きいということです。例として、y=x_n+1としてa=3.8の時の図を示すと次になります。

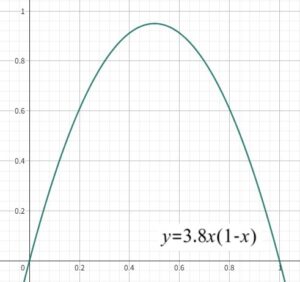
つまり人口の増加の割合はx=1/2までは増えていき、それから減っていくということを示しています。ロジステック関数(式5)と対応しています。
最初人口の数という集合を扱ってきたのですが、ここへきて人口の割合、x_nからx_n+1というような状態の遷移を扱う集合に変わったと解釈できます。このようにある集合から別の集合に変わることを写像と言います。人口Nの扱いからx_nを扱うようになったので、ロジステック写像なわけです。パイこね変換の場合は最初かx_nとx_n+1の関係を扱っており、同じx_nの集合の値がどう変わるかを問題にしていたのです。ですのでこれは写像でなくて変換といいます。人口の増減について話している時はＮに対して微分方程式を解くということが重要でした。この概念（この集合）でいくら考えても以下で話すカオスはでてきません。これをx_nに写像するから、もともとは人工の数を扱っているにも関わらず、カオスという概念で話すことができるようになります。このように写像は奥に潜む構造を見つけることができるとてもに強力な操作です。
この図とパイこね変換の図を見ていただくと、非常によくにていることがわかると思います。パイこね変換は直線の織れ曲がりでしたが、それが２次式になっているということです。これからカオスの特性が生じるものと予測します。しかしいつもカオスになるわけでなく、aによっているというパイこね変換にはなかった性質が現れます。これを図にしたのがWikipediaにありました。
https://ja.wikipedia.org/wiki/%E3%83%AD%E3%82%B8%E3%82%B9%E3%83%86%E3%82%A3%E3%83%83%E3%82%AF%E5%86%99%E5%83%8F
をみていだだくと、a（=r)に対してどう変化するかを描いています。3.57<=a<=4の時カオスになります。aの値は4以上ありません。これはx_n+1が負になるためです。
次にカオスの説明によく登場する分岐ダイアグラムを描いてみましょう。ロジステック写像の式(8)において、横軸をa, 初期値x(0)=0.5とした時のx_n+1を描いたものです。

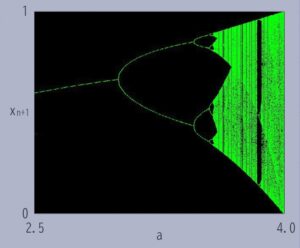
最初x_n+1はaに対して1つの値しかとりませんが、それが分岐していって、3.57以上になると様々な値を取るようになりカオス状態となります。つまり繁殖率が大きくなると人口増加の割合は大きく変化し予測できなくなります。これをどう解釈すればよいかということですが、式(4)は人口が何らかの原因で飽和することを示しています。例えば食糧や病気、土地の広さ等により制限を受けるということです。つまり繁殖率は高いが、直ぐに食料がなくなったりする状況では、急速に増えるが支えられず直ぐに減少します。しかし繁殖率が高いのですぐに増えます。このような乱高下を繰り返すことになるということです。この動きはカオスですのでどう変化するのか予測できない、ということです。しかしこの大きな変動は、ロジステック関数(式(5))には反映されていません。x_n+1の離散化された値は人口の割合をあらわしているのに対して、ロジステック関数のNは人口をあらわしています。そして微分方程式の一般解は定常状態をあらわします（時間が十分に経った状態です）。人口の割合が非常に激しく変動しても人口全体の定常状態は飽和して安定することを述べています。これは、一人一人の人間にとっては、乱高下する激しい生存の状態になったとしても、人口としては飽和した一定の値に落ち着くということです。より一般化して話すなら、微分方程式で安定だったとしても、個々のレベルではダイナミックな変動をしている場合もありうる。ということです。そして重要な点として、Nの人口の話から、x_n+1の離散化された状態に写って議論したわけですが、これが写像です。集合でいうとNを扱う集合から、x_n+1を扱う別の集合に写ったということです。そしてこの写像によって、ダイナミックな変動を扱うことができるようになったのです。

このプログラムを次に示します。

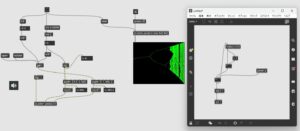
これはMAXによって描いています。MAXにはgen~と言う標準オブジェクトで実現できない処理をする拡張機能があります。gen~にはhistoryという過去の値を保持するオブジェクトがあり（Touchdesignerのfeedback CHOPに相当している機能です）、これが再帰のフィードバックを扱うことを容易にしています。historyを使うとロジステック写像の式を直接オブジェクトを使って記述することができます。

ローレンツアトラクター

気象学者のローレンツが大気の変動モデルを研究していて、非常に単純化した式を考察しました。それが次の式です。

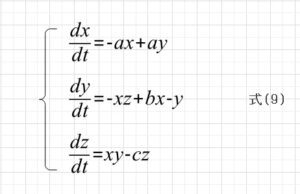
ローレンツはパラメータa=10, b=28, c=8/3の時に、奇妙なふるまいが生じることを発見しました。この奇妙なふるまいがカオスです。ここではローレンツがどのようにしてこの式を導いたかということではなく、アトラクターという新たに登場する概念について、そしてカオスはアトラクター上にどのように現れるのかを述べていきます。つまり図で示すとカオスはこんな感じになる。ということをこの例で示そうと思います。カオスはこれまで説明してきたように、決定論の秩序があるにもかかわらず予測不能になる現象です。アトラクターはその秩序のあるという部分を象徴していますが、そこにどのようにカオスが現れるのかも示しています。これまで述べたロジステック写像の場合は一次元でした。ランダムと異なりアトラクターが無いわけではありませんが、視覚的にインパクトのあるアトラクターとはなりません。その点ローレンツアトラクターは綺麗です。
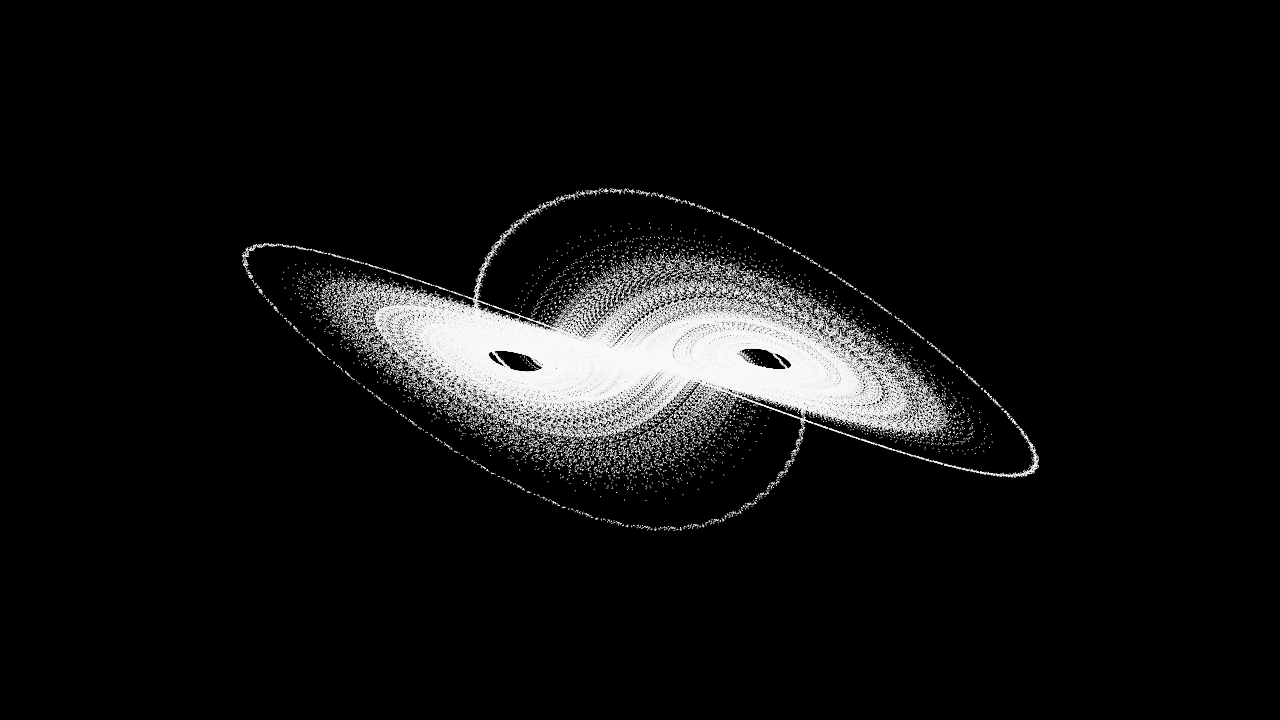
次の動画はローレンツアトラクターと呼ばれているものです。これは上の式(9)の微分方程式を数値的に解いて、得られた(x,y,z)を時間に対してプロットした図です。Touchdesignerで描きました。

アトラクターというのは、引き付ける、魅力という意味です。ローレンツアトラクターの場合、2つの円ができ、そこに引き付けられているように見えます。アトラクターは例えば、リミットサイクルの場合ですと、一定の周期的な軌道に引き寄せられます。リミットサイクルはカオスではありません。アトラクターはカオスを説明する特別な言葉ではありません。カオスと言う意味では、アトラクターは構造と関係しており重要ですが、カオスかどうかと言う点では、アトラクターに次の特徴を持つことが重要です。それはパイこね変換やロジステック写像で話していたことと同じですが、まとめると、
１．アトラクターはいつまでも少しずつ違う値を描く。収束しない。
２．初期値で描き方が大きく違う。アトラクターの全体的な形は初期値をかえても変わりません。通る道は同じだが、いつ通るかがわからない。
というのがアトラクターに現れるカオスです。
またアトラクターは一見ポテンシャルのように見えます。つまりそこへたまり、あるエネルギーが与えれらると飛びだすことができる、というようにです。しかしポテンシャルではありません。アトラクターは「吸引領域」のようなもので、カオスの場合、そこへ引き付けられ、その領域で軌道は永続的に複雑な動きをし続けます。一番低い底へたまっていくというものではありません。また複数のアトラクターがある場合は、吸引されるアトラクターが変わっていくということもあります。

それでは、上記の2つの特性が分かるように、初期値の違いう２つのローレンツアトラクターの計算例を示します。。白と黄色でアトラクターを描がいています。初期値の違いは、一番最初にでてくる場所の違いです。よく見ていただくとわかります。右上のボタンを押していただいて、拡大してみてください。

よく見ていただくと、２つのプロットが動いていることがわかります。初期値は近いので最初ほとんど重なって動いているように見えますが、次第に離れていく様子がわかります。そして時間がたてば異なる動き方をしていることがわかります。しかし2つのアトラクターはほとんど同じ映像になっていきます（収束するわけではないので、すこしづつ軌道は違っています）。上記の１．２の特徴が表れていることが見て取れるでしょう。時間がたてば通る道は結局わずかしか違わないのですが（これが決定論的なところです）、いつそこを通るのかということが分からない。ということです。これは山登りに例えることができます。通常山へ登る山道は決まっており、その道の中央を通るか端を通るかといったような違いがあるくらいです。しかしいつその場所を通るのかというのは分からないのです。
次に示すのは、カオスとならない場合の例です。ローレンツのパラメータのa=1の時の映像です。アトラクターに収束していき固定されます。これはカオスではありません。

最後に、ロジステック方程式(式4)とローレンツの方程式(式9)との違いについて述べます。ロジステック方程式ではカオスの現象が出てきませんでした。カオスを反映させるには離散化する写像が必要でした。一方、ローレンツの方程式を数値的に説いた映像では、カオスの初期値の違いや軌道の微妙な違いを反映しておりました。これは、ロジステック方程式は線形微分方程式で、ローレンツの方程式は非線形微分方程式だからです。カオスは非線形微分方程式から出てくる非線形現象です。ロジステック写像を再度解釈すると、これは線形微分方程式から非線形の離散化微分方程式への変換であったのです。

Touchdesignerのプログラムは「「https://www.youtube.com/watch?v=PvhLYosLHus」を真似ています。しかしこの動画では初期値を変えることができません。初期値を変更できるようにしております。Touchdesignerの中では、pythonとGLSLというコードで書くプログラムを併用して使うことができます（私自身はまだ自由に扱えるわけではありません）。オペレータでつなぐビジュアルプログラムとコードで書くプログラムとの連携は非常に強力です。高速で映像を伴うプログラムが簡潔に作製することができます。GLSLはこれまでのblogでも使ってきましたが、それは主に表面の映像を変えるシェーダーとして使ってきました。今回のように微分方程式を記述するといったことにも長けています。